해싱(Hashing)
키 값을 특정한 계산을 통하여 나온 결과를 주소로 사용하여 값에 접근하는 과정
- 키와 벨류를 매핑시키는 과정
- 빠른 탐색과 삽입,삭제를 통하여 항목간의 관계를 모형화 하는데 유용함
- 키 값에 직접 산술적인 연산을 적용, 테이블의 주소를 계산하여 접근
- 키값의 연산에 의해 직접 접근이 가능한 구조를 해시 테이블 이라 부르고 테이블을 이용한 탐색

추상 자료형 사전구조
- 인터페이스와 기능 구현을 분리한 자료형
- 기능 구현구분을 명시하지 않아 사용 시에는 기능이 어떻게 돌아가지 몰라도 되는 편리함을 가짐
- 대표적으로 스택 큐 연결리스트 딕셔너리
- 해시 테이블은 인터페이스만을 보았을때는 데이터 식별자로 숫자 뿐만아니라 문자열 파일등을 받아와 Value를 연상
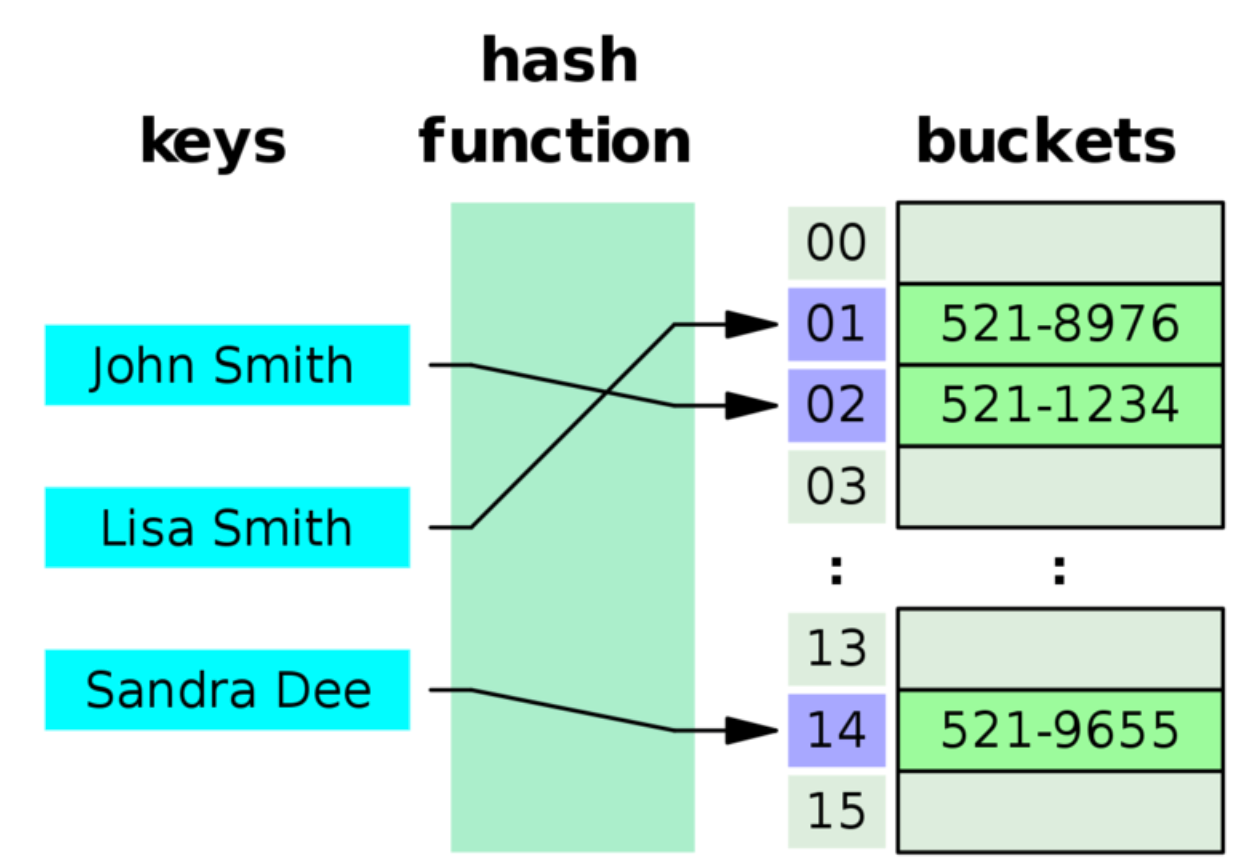
해싱의 구조
- 어떤 항목의 탐색 키만을 가지고 바로 항목이 저장되있는 배열의 인덱스를 결정하는 기법
- 탐색키를 작은 정수로 매핑 시키는 함수가 필요
- 예를들어 영어사전에서는 단어가 탐색키가 되고 이 단어를 해싱 함수를 이용하여 적절한 정수 i로 변환한 다음,
배열 요소 ht[i]에 단어의 정의를 저장하는 것

해시 테이블의 구조
해시테이블은 n개의 버킷으로 이루어지는 테이블로서 n-1개의 원소를 가짐
하나의 버킷은 s개의 슬롯을 가질 수있으며, 하나의 슬롯에는 하나의 항목이 저장됨
하나의 버킷에 여러개의 슬롯을 두는 이유
서로 다른 두 개의 키가 해시 함수에 의해 동일한 해시 주소로 변활 될 수 있으므로
여러 개의 항목을 동일한 버킷에 저장하기 위함

버킷과 슬롯
버킷
- 여러개의 슬롯을저장하는 레코드 형태의 자료 구조
- 버킷의 갯수는 고정적
슬롯
- 해시와 매핑되는 값이 저장되어 있는 공간
- 하나의 버킷 안에는 여러개의 슬롯이 존재할 수 있음
- 슬롯은 하나이상의 값을 저장할 수 있음
해시 테이블이 사용되는 이유
- 평균적으로 탐색,삽입,삭제에 O(1) 의 시간 복잡도를 가짐
- 어떤 항복과 다른 항목의 관계를 모형화하는데 좋음
- 무한한 데이터를 유한한 키값으로 관리할 수 있음
실제의 해싱
해시 테이블의 크기가 제한되어있으므로 하나의 탐색키당 해시 테이블에서 하나의 공간을 할당 할 수가 없음
=> 해싱함수가 필요
충돌과 오버플로우 발생
=> 슬롯의 숫자도 무한이 아니기 때문, 해싱함수에서 나온 결과가 같을 경우 충돌 발생
해시함수
- 탐색 키를 입력받아 해시주소를 생성
- 만들어진 해시 주소가 배열로 구현된 해시 테이블의 인덱스가 됨
- 인덱스 위치에 자료를 저장 할 수도 있고 저장된 자료를 꺼낼 수도 있음
해시함수 특징
1. 어떤 입력값에도 항상 고정된 길이의 해시값을 출력 (동일한 값이 입력되면 언제나 동일한 출력값을 보장)
2. 눈사태 효과: 입력값의 아주 일부만 변경되어도 전혀 다른 결과 값을 출력
3. 출력된 결과 값을 토대로 입력값을 유추할 수 없음
좋은 해시 함수의 조건
- 충돌이 적어야 함
- 해시 함수값이 해시 테이블의 주소 영역 내에서 고르게 분포되어야 함
- 계산이 빨라야 함
함수의 종류
1. 제산함수 : h(k)=k mod M (해시테이블 M의 크기는 소수prime number)
2. mid - square : 키를 제곱하여 버킷을정함,
3. 폴딩 : 키를 몇몇 부분으로 나눈 후 그 값을 더하여 해시 함수의 결과를 도출
3-1) 시프트 폴딩 : 부분을 일정하게 나눈 후 더하는 방식
k가 12345678910일때 3개의 10진수로 나눈다면 h(12345678910) = 123 + 456 + 789 + 10이 되고
더하게 되면 1378이 되므로 h(12345678910) = 1,378
3-2) 경계 폴딩 : 부분의 경계를 뒤집어서 계산
k가 12345678910이고 3개의 10진수로 나눈다면 h(12345678910) = 123 + 654 + 789 + 01이며 결과는 1,567
456과 10이 뒤집혀져 있다.
충돌
다른내용의 데이터가 같은 키를 갖는 상황
같은 키 값을 가지는 데이터가 생기는 것은 특정 키의 버켓에 데이터가 집중된다는 뜻
너무 많은 해시 충돌은 해시 테이블의 성능을 떨어뜨림
- 해시함수의 입력값은 무한하지만 출력값의 가짓수는 유한하므로 해시충돌은 반드시 발생 (*비둘기집 원리)
- 클러스터링(Clustering) : 연속된 레코드에 데이터가 몰리는 현상
- 오버플로우(Overflow) : 해시 충돌이 버킷에 할당된 슬롯 수보다 많이 발생하면 더 이상 버킷에 값을 넣을 수 없는 현상
*비둘기집 원리 : n+1개의 물건을 n개의 상자에 넣은 경우, 최소한 한 상자에는 그 물건이 반드시 두 개 이상 존재
충돌 해결방법
1. 체이닝
버킷 내에 연결리스트를 할당하여 버킷에 데이터를 삽입
해시 충돌이 발생하면 연결리스트로 데이터들을 연결
- 체이닝의 경우 버킷이 꽉 차더라도 연결리스트로 계속 늘려가기에 데이터의 주소값은 바뀌지 않음

2. 개방 주소법
해시 충돌이 일어나면 다른 버킷에 데이터를 삽입하는 방식 (데이터의 주소값이 바뀜)
삭제의 경우 충돌에 의해 저장된 데이터가 검색되지 않을 수 있음
=> 삭제한 위치에 더미노드를 삽입 (다음 위치까지 연결 해 주는 역할)
더미 노드가 많아지면 버킷을 연속적으로 검색해야 하기 때문에
더미 노드의 개수가 일정 이상이 되었을경우 주기적으로 새로운 배열을 만들어 재해시를 해줘야 성능을 유지 가능
2.1 선형 탐색
해시 충돌시 다음 버킷, 혹은 몇 개를 건너뛰어 데이터를 삽입

장점 : 구조가 간단하고 캐시의 효율이 높음
단점 : 최악의 경우 해시테이블 전체를 검색해야 하는 상황이 발생, 데이터의 클러스터링에 가장 취약
2.2 2차 검색법
원래 저장할 위치로부터 떨어진 영역을 차례대로 검색하여 첫번째 빈 영역에 키를 저장하는 방법

- 선형 검색법에서 발생하는 제1 밀집문제를 제거하는 방법
- 같은 해시값을 갖는 키에 대해서는 제 2 밀집 발생
- 캐시 효율과 클러스터링 방지 측면에서 선형 검색법과 2중해싱의 중간정도의 성능
2.3 이중 해시
해시 충돌시 다른 함수를 한번 더 적용한 결과를 이용
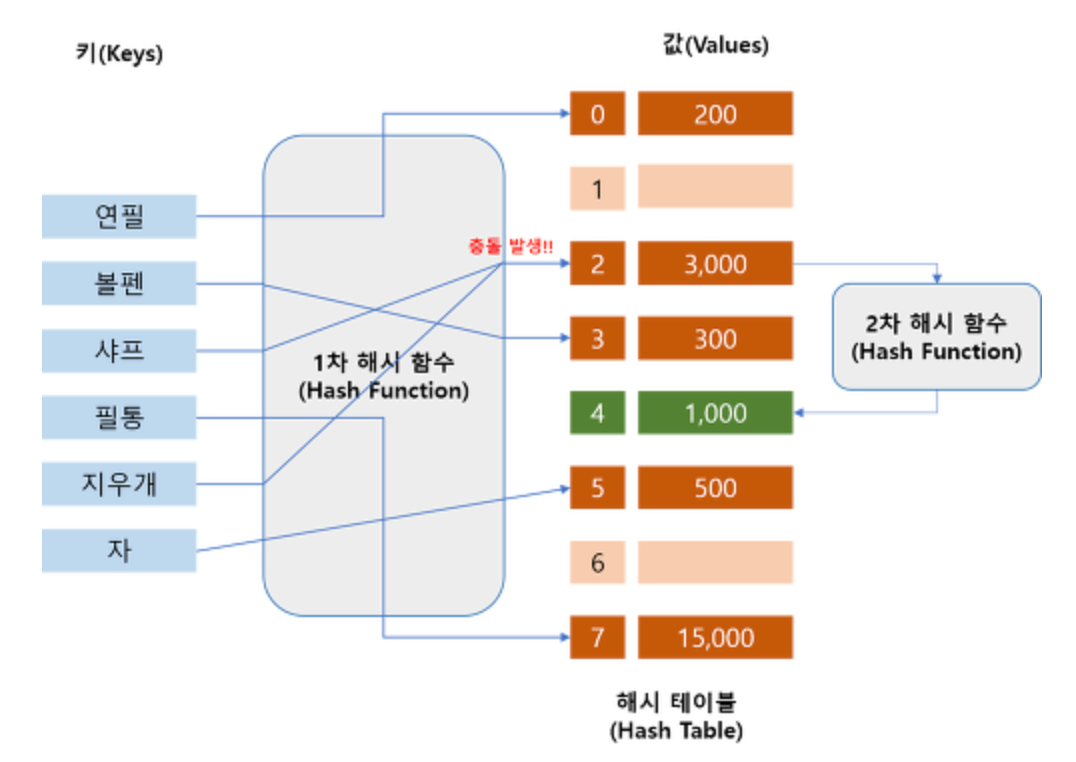
- 캐시 효율은 떨어지지만 클러스터링에 영향을 거의 받지 않음
- 가장 많은 연산량을 요구
체이닝과 선형 탐색의 비교

체이닝 : 연결 리스트를 사용하여 복잡한 계산식을 개방주소법에 비해 적게 사용
해시테이블이 채워질수록 성능 저하가 선형적으로 발생
개방주소법 : 포인터가 필요 없고 지정한 메모리 외 추가적인 저장공간도 필요 없음
삽입, 삭제시 오버헤드가 적고, 저장할 데이터가 적을 때 더 유리
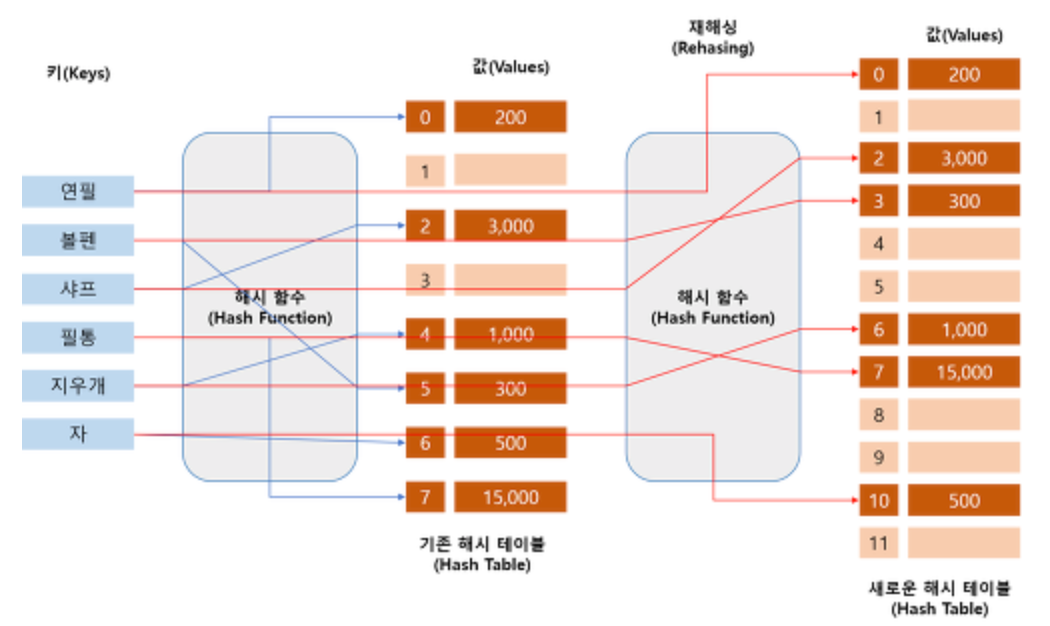
리사이징
새로운 배열에 기존 배열의 키를 새롭게 재 해싱
개방주소법에서 사용되는 고정 크기의 배열이 가득 차거나 체이닝의 연결 리스트가 길어지게되면
검색 효율이 떨어지기 때문에 버킷의 갯수를 늘려주는 방법
해싱의 성능 분석
해싱의 시간복잡도는 O(1)
충돌이 전혀 일어나지 않는 상황에서만 가능
따라서 실제 해싱의 탐색 연산은 보다 느려짐
'자료구조' 카테고리의 다른 글
| 분할 정복 알고리즘 (Devide and Conquer) (0) | 2021.05.12 |
|---|---|
| 그리디 알고리즘 (Greedy Algorithm) (0) | 2021.05.12 |
| B-트리, B+트리, 2-3 트리, 2-3-4 트리 (0) | 2021.05.12 |
| AVL 트리 (AVL Tree) (0) | 2021.05.11 |
| 이진 탐색 트리 (Binary Search Tree) (0) | 2021.05.10 |