이진 탐색 트리 (Binary Search Tree)

이진 탐색 트리란

이진탐색(binary search)과 연결리스트(linked list)를 결합한 자료구조

왼쪽 자손 노드에는 현재 노드 보다 작은 값을, 오른쪽 자손 노드에는 현재 노드보다 큰 값을 넣는 방식의 트리
이진탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안
연결리스트의 경우 자료 입력, 삭제에 필요한 계산복잡성은 O(1), 탐색하는 데에는 O(n)의 계산복잡성이 발생
두개의 이점을 합치기 위해 만든 자료구조

https://coding6467.tistory.com/10

- 각 노드의 왼쪽 서브트리에는 해당 노드의 값보다 작은 값을 지닌 노드들로 이루어짐
- 각 노드의 오른쪽 서브트리에는 해당 노드의 값보다 큰 값을 지닌 노드들로 이루어짐
- 중복된 노드는 없어야 함
- 왼쪽 서브트리, 오른쪽 서브트리 또한 이진 탐색 트리
- 이진탐색트리를 순회할 때는 중위순회(inorder) 방식을 사용

탐색 

부모노드가 왼쪽 자식노드보다 크거나, 오른쪽 자식노드보다 작은점에 착안하면 효율적인 탐색 가능

https://coding6467.tistory.com/10

ex) 탐색 10

1. 루트노드 7과 10을 비교
2. 10은 7보다 크므로 왼쪽 서브트리(1, 3, 5)는 고려할 필요가 없음
3. 오른쪽 서브트리의 루트노드 8과 10을 비교
4. 10은 8보다 큼
5. 루트노드 10과 10을 비교
6. 탐색 완료

 

삽입

새로운 데이터는 트리의 잎새노드에 붙임

1. 삽입하려는 데이터를 탐색
2. 탐색이 실패한 지점에 해당 노드 삽입

https://coding6467.tistory.com/10

ex) 삽입 4

7과 3사이에 4를 추가해도 이진탐색트리의 속성이 깨지지 않으나,
이진탐색트리가 커질 경우 트리의 중간에 새 데이터를 삽입하게 되면 서브트리의 속성이 깨질 수 있음
그래서 삽입 연산은 잎새 노드에서 진행 됨

 

삭제

이진 탐색 트리 관련 알고리즘 중 가장 복잡
1. 탐색을 진행
2. 노드를 탐색했다면, 아래의 3가지 경우를 고려
  1) 삭제하려는 노드가 단말노드일 경우 (자식 노드가 없을 경우)
  2) 삭제하려는 노드가 하나의 서브트리만 가지는 경우 (왼쪽 혹은 오른쪽 둘 중 하나만)
  3) 삭제하려는 노드가 두 개의 서브트리를 모두 가지고 있는 경우

1) 삭제하려는 노드가 단말노드일 경우

https://coding6467.tistory.com/10

부모 노드를 찾아서 부모 노드 안의 해당 링크(그림의 경우 오른쪽 링크) 필드를 NULL로 만들어서 연결을 끊어줌
동적으로 할당된 노드였을 경우, 메모리 반납을 하고 링크필드를 NULL로 만들어 줌

2) 삭제하려는 노드가 하나의 서브트리만 가지는 경우

https://coding6467.tistory.com/10

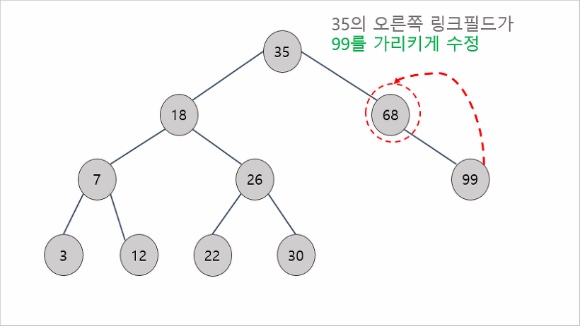
ex) 68을 가지고 있는 노드 삭제
35를 가지고 있는 부모 노드의 오른쪽 링크 필드가 99를 가리키게 수정
동적할당된 노드였다면, 68을 먼저 반납해주고 부모의 오른쪽 링크에 99를 붙임

3) 삭제하려는 노드가 두 개의 서브트리를 모두 가지고 있는 경우

https://coding6467.tistory.com/10

ex) 18을 가지고 있는 노드 삭제
왼쪽 서브트리에 있는 값 중 가장 큰 값, 혹은 오른쪽 서브트리에 있는 값 중 가장 작은 값을 가지고 있는 노드를 연결
=> 트리의 변동성을 최소화하기 위함

시간 복잡도

(탐색 = 삽입 = 삭제)
균등 트리 : 노드 개수가 n개일 때 O(logn)
편향 트리 : 노드 개수가 n개일 때 O(n)