다익스트라 알고리즘 (Dijkstra Algorithm)

다익스트라 알고리즘이란

음의 가중치가 없는 그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘

https://chanhuiseok.github.io/posts/algo-47/

다익스트라 알고리즘 과정

1. 출발점으로부터의 최단거리를 저장할 배열 d[v] 생성.
   출발 노드에는 0을, 출발점을 제외한 다른 노드들에는 매우 큰 값 INF를 채움
2. 현재 노드를 나타내는 변수 A에 출발 노드의 번호를 저장
3. A로부터 갈 수 있는 임의의 노드 B에 대해, d[A] + P[A][B]와 d[B]의 값을 비교
4. 만약 d[A] + P[A][B]의 값이 더 작다면, d[B]의 값을 이 값으로 갱신
5. A의 모든 이웃 노드 B에 대해 이 작업을 수행
6. A의 상태를 "방문 완료"로 바꾼다. 더 이상 A는 사용하지 않음
7. "미방문" 상태인 모든 노드들 중, 출발점으로부터의 거리가 제일 짧은 노드 하나를 골라서 그 노드를 A에 저장
8. 도착 노드가 "방문 완료" 상태가 되거나, 더 이상 미방문 상태의 노드를 선택할 수 없을 때까지, 3~7의 과정을 반복

 

https://hsp1116.tistory.com/42

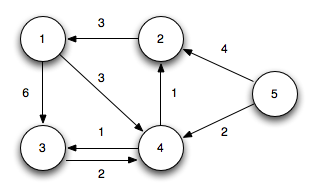
5 => 2 구해지는 과정

5 => 2는 4의 가중치를 가집니다. 
dist[2] = 4;

5 => 4는 2의 가중치를 가집니다.
dist[4] = 2;

5=>2와 5=>4=>2를 비교
if(dist[2] > dist[4] + adj[4][2]){
  dist[2] = dist[4] + adj[4][2]; 
}

if(4 > 2 + 1) // true
dist[2] = 2 + 1;

dist[2]는 3이 됩니다.

 

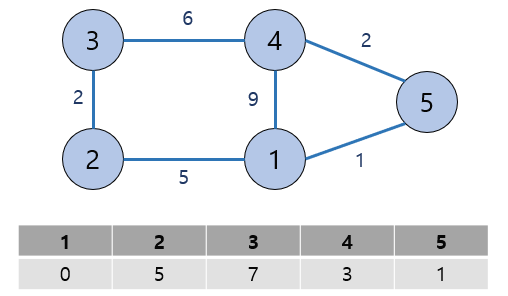
다익스트라 알고리즘을 통한 결과값

https://hsp1116.tistory.com/42

우선순위 큐 기반 다익스트라 알고리즘

모든 정점을 우선순위 큐에 넣어서 가장 짧은 경로 부터 탐색할 수 있는 알고리즘

일반 다익스트라 알고리즘보다 구현이 어려우나 시간이 빠름

 

시간 복잡도 

다익스트라 알고리즘 : O(V^2)

우선순위 큐 기반 다익스트라 알고리즘 : O(ElogV)