728x90
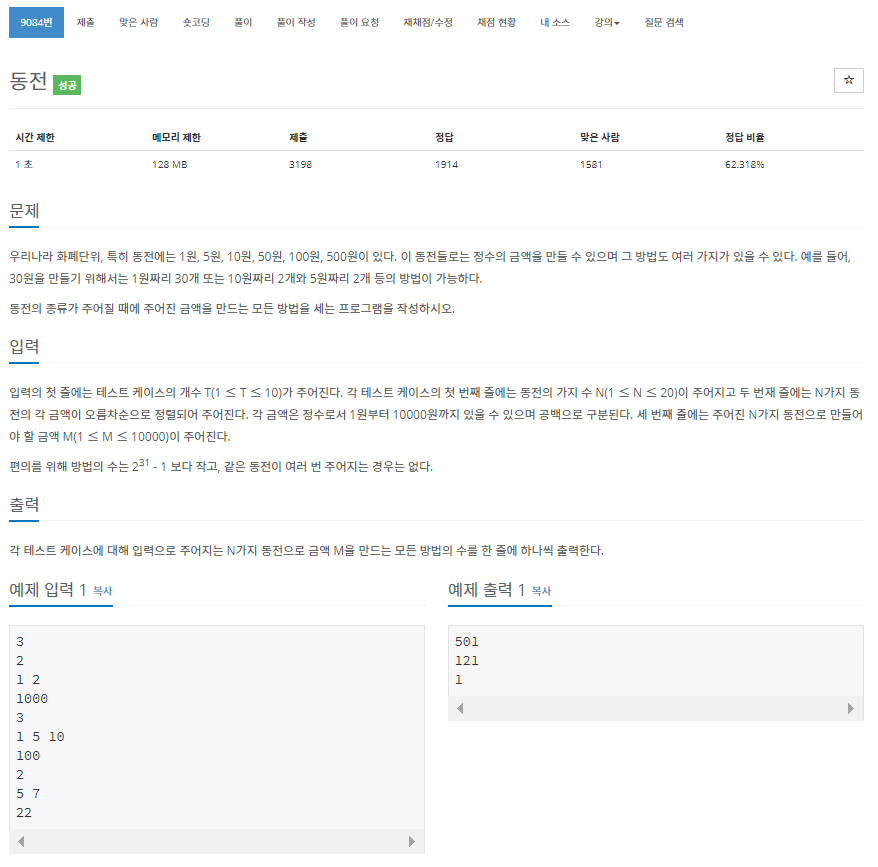
여러 단위의 동전을 이용해서 찾고자 하는 동전을 만들때
만들 수 있는 경우의 수를 구하는 문제입니다.
10원을 2원, 3원, 5원으로 구한다고 하면
2원부터 구할때
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 2 | X | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 3 | ||||||||||
| 5 |
3원을 구할때
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 2 | X | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 3 | X | X | 1 | 0 | 1 | 2 | 1 | 1 | 2 | 2 |
| 5 |
5원을 구할때
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 2 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 3 | ||||||||||
| 5 |
와 같이 구할 수 있습니다.
처음 2의 배수에 +1을 해줍니다.
3을 구할땐 3의 배수에 +1을 해주고, 2의 배수이면서 3을 더했을때 나오는 값의 위치에 +1을 해주면 됩니다.
5를 구할땐 3을 구할때 했던 방식을 그대로 해주면 됩니다.
코드로 볼때
memo[0] = 1이 들어가있습니다.
그 후
memo[j] += memo[j - coin[k]];의 코드가 반복되면서 실행이됩니다.
처음에는 memo[0]의 값이 들어가게됩니다. 이는 배수값에 +1의 역할을 합니다.
두번째는
memo[j] += memo[j - coin[k]];
현재 위치에서 - 현재 찾고있는 동전의 값을 뺀 인덱스를 접근해서 그 값을 가져옵니다.
이를 통해서 각 동전의 값에 대한 합에 대한 경우의수를 구하게 됩니다.
#include
using namespace std;
int coin[20]; // 동전
int memo[10001]; // 메모
void init() { // 초기화
for (int i = 0; i < 20; ++i) {
coin[i] = 0;
}
for (int i = 0; i < 10001; ++i) {
memo[i] = 0;
}
memo[0] = 1; // 배수 값을 증가시켜주기 위함
}
int main(int argc, char *argv[])
{
int cycle; // 반복 실행 횟수
int coinNum = 0; // coin 종류 갯수
int findCoin; // 찾는 coin 값
cin >> cycle;
for (int i = 0; i < cycle; ++i) {
init();
cin >> coinNum;
for (int j = 0; j < coinNum; ++j) {
cin >> coin[j];
}
cin >> findCoin;
for (int k = 0; k < coinNum; ++k) {
for (int j = coin[k]; j <= findCoin; ++j) {
memo[j] += memo[j - coin[k]]; // 현재 동전의 경우의 수에 그전의 동전들의 경우의 수를 더해줌
}
}
cout << memo[findCoin] << endl;
}
return 0;
}'알고리즘' 카테고리의 다른 글
| [C++] 백준 2579번 계단 오르기 (0) | 2019.05.03 |
|---|---|
| [C++] 백준 2631번 줄세우기 (0) | 2019.05.01 |
| [C++] 백준 1965번 상자넣기 (0) | 2019.04.10 |
| [C++] 백준 1065번 한수 (0) | 2019.04.07 |
| [C++] 백준 2446번 별 찍기 - 9 (0) | 2019.04.06 |