728x90
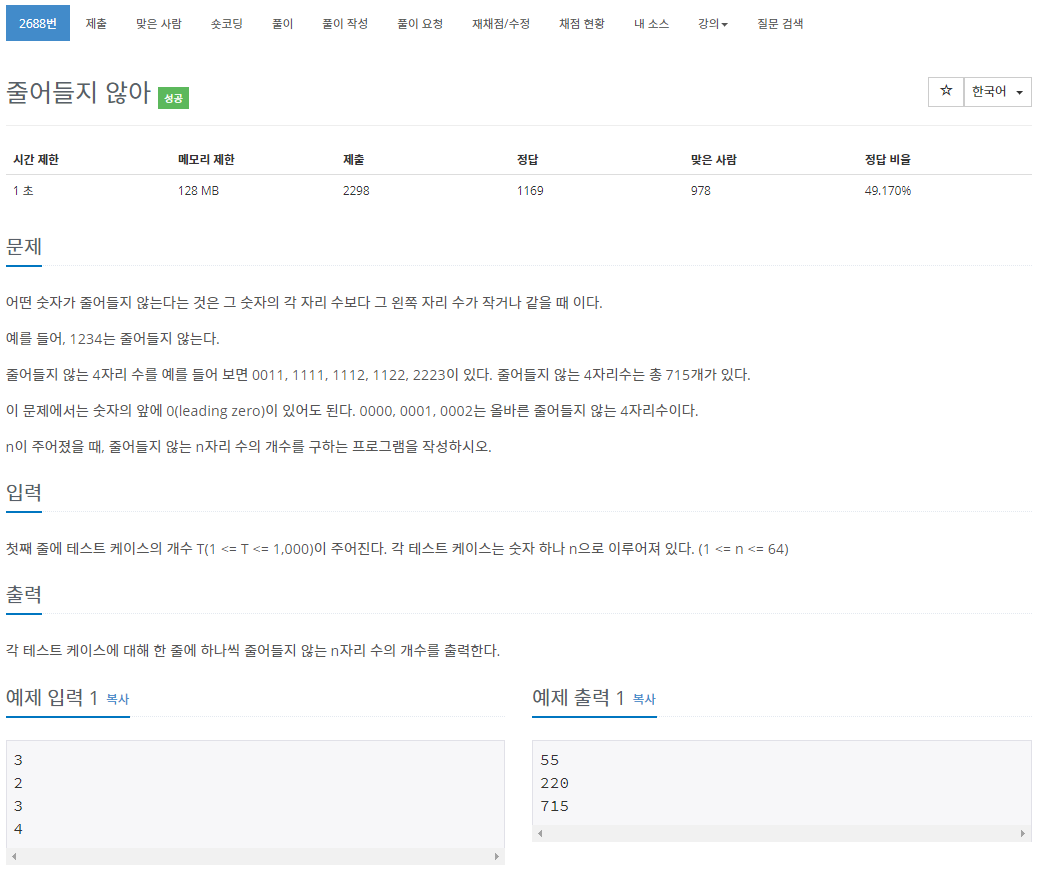
다이나믹 프로그래밍 문제입니다.
각 자리수가 한자리 부터 모든 경우의 수를 채우고
다음은 두자리 ... 세자리 ... 네자리 ... n자리 까지 채웁니다.
A자리는 A-1자리에서 뒷자리수가 현재 수보다 작은 것들의 합 + 1을 해주면됩니다.
이렇게 되면 9의경우 0~8까지 수를 전부 더한 뒤 + 1을 해줘야하고
8도 0~7까지 수를 전부 더한 뒤 +1을 해줘야합니다.
여러 번 반복해야하는 경우가 생기므로 다른 방법을 찾아보았습니다.
뒷자리수가 B일때 B-1은 나머지 DP[B]의 값을 제외하고 모든 값을 가지고 있습니다.
그래서 DP[B] = DP[B-1] + DP[B]라는 점화식을 세울 수 있습니다.
(뒷자리수)
DP[1] = DP[1] + 1
DP[2] = DP[2] + DP[2 - 1] + 1
DP[3] = DP[3] + DP[3 - 1] + 1
...
DP[9] = DP[9] + DP[9 - 1] + 1
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int main(int argc, char* argv[])
{
int ts;
int n;
long long result = 0;
long long DP[10];
cin >> ts;
while (ts--) {
result = 0;
cin >> n;
fill(DP, DP + 10, 1);
DP[0] = 0;
for (int i = 2; i <= n; ++i) {
DP[1] = DP[1] + 1;
for (int j = 2; j <= 9; ++j) {
DP[j] = DP[j - 1] + DP[j];
}
}
for (int i = 0; i <= 9; ++i) {
result += DP[i];
}
cout << result + 1 << endl;
}
return 0;
}'알고리즘' 카테고리의 다른 글
| [C++] 백준 1620번 나는야 포켓몬 마스터 이다솜 (1) | 2019.12.10 |
|---|---|
| [C++] 백준 10597번 순열장난 (0) | 2019.12.04 |
| [C++] 백준 13904번 과제 (0) | 2019.11.27 |
| [C++] 백준 2457번 공주님의 정원 (1) | 2019.11.26 |
| [C++] 백준 11058번 크리보드 (3) | 2019.11.26 |