728x90
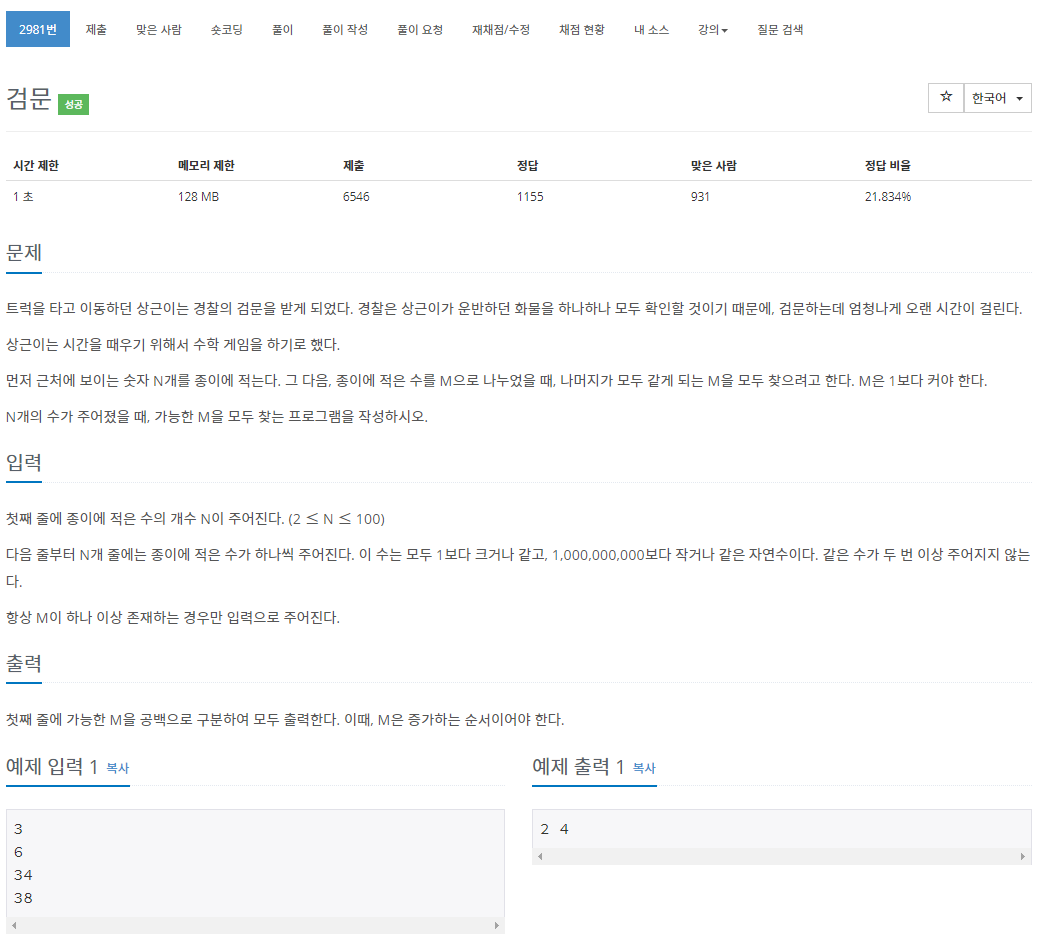
N개의 숫자들을 M으로 나누었을 때 나머지가 모두 같은 경우의 M을 모두 찾는 문제입니다.
v[i]를 M으로 나눈 몫과 나머지는 다음으로 나타낼 수 있습니다.
v[i] = M * 몫[i] + 나머지
나머지는 같은 경우를 찾기 때문에 나머지를 빼는 방식으로
가능한 공식에 대해서 해를 찾습니다.
v[i-1]에 대해서 위의 공식을 이용해서 빼줍니다.
v[i] - v[i-1] = M * (몫[i] - 몫[i - 1]) + (나머지 - 나머지)
v[i] - v[i-1]이 정답이 되는데
모든 v[i] - v[i-1]에 대해서 최대 공약수를 찾고
그 약수를 출력해서 문제를 풀었습니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int GCD(int a, int b)
{
if (a % b == 0) {
return b;
}
return GCD(b, a % b);
}
int main(int argc, char *argv[])
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int N;
int x;
vector<int> v;
vector<int> num;
cin >> N;
for (int i = 0; i < N; i++) {
cin >> x;
v.push_back(x);
}
sort(v.begin(), v.end());
int gcd = v[1] - v[0];
for (int i = 2; i < N; i++) {
gcd = GCD(gcd, v[i] - v[i - 1]);
}
for (int i = 2; i * i <= gcd; i++) {
if (gcd % i == 0) {
num.push_back(i);
num.push_back(gcd / i);
}
}
num.push_back(gcd);
sort(num.begin(), num.end());
num.erase(unique(num.begin(), num.end()), num.end());
for (int i = 0; i < num.size(); i++) {
cout << num[i] << " ";
}
cout << "\n";
return 0;
}'알고리즘' 카테고리의 다른 글
| [C++] 백준 11050번 이항 계수 1 (0) | 2019.09.03 |
|---|---|
| [C++] 백준 3036번 링 (0) | 2019.09.03 |
| [C++] 백준 2609번 최대공약수와 최소공배수 (1) | 2019.09.02 |
| [C++] 백준 11653번 소인수분해 (0) | 2019.09.02 |
| [C++] 백준 1037번 약수 (0) | 2019.09.02 |