[Java] 백준 11055번 가장 큰 증가하는 부분 수열

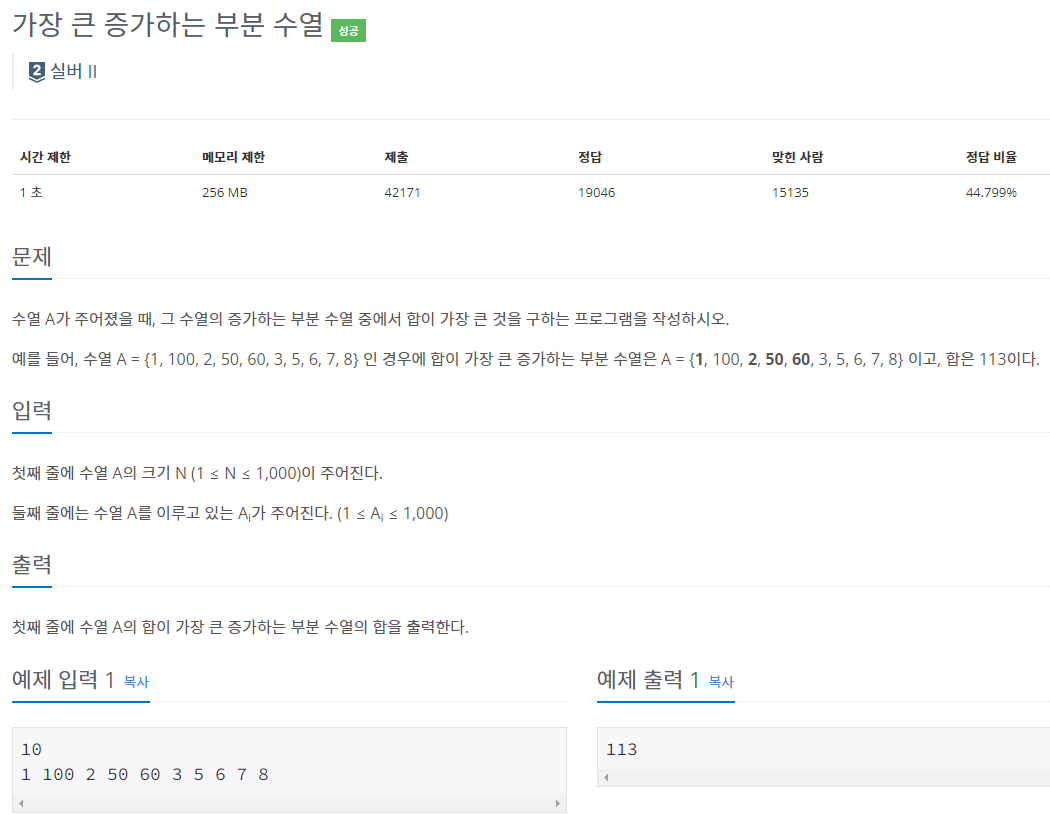
다이나믹 프로그래밍 문제입니다.
수열이 주어졌을 때 가장 큰 증가하는 부분 수열의 합을 출력합니다.

https://j3sung.tistory.com/941

[Java] 백준 11053번 가장 긴 증가하는 부분 수열

위의 문제와 거의 동일한 문제입니다.

위 문제는 DP값에 길이를 넣었다면 현재문제는 DP값에 합을 넣어주었습니다.

DP[j] = Math.max(DP[j], arr[j] + DP[i]);

위의 점화식을 사용해서 DP값을 찾아내어 결과값을 출력해주었습니다.

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;

public class Main {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st = null;
		
		int ans = 0;
		int n = Integer.parseInt(br.readLine());
		int[] arr = new int[n+1];
		int[] DP = new int[n+1];
		
		st = new StringTokenizer(br.readLine());
		for(int i=1; i<=n; ++i) {
			arr[i] = Integer.parseInt(st.nextToken());
			DP[i] = arr[i];
		}
		
		for(int i=0; i<=n; ++i) {
			for(int j=i+1; j<=n; ++j) {
				if(arr[i] < arr[j]) {  
					DP[j] = Math.max(DP[j], arr[j] + DP[i]);
				}
			}
		}
		
		for(int i=1; i<=n; ++i) {
			ans = Math.max(ans, DP[i]);
		}		
		
		bw.write(ans + "\n");		
		bw.close();
	}
}