유니온 - 파인드 알고리즘
서로 중복되지 않는 부분집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
- 공통 원소가 없는, 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 자료구조
- 집합을 구현하는데 트리구조를 이용하여 구현
- 여러 노드가 존재할때 선택한 두 노드가 서로 같은 그래프에 속하는지 판별하는 알고리즘
- find : x가 어떤 집합에 포함되어있는지 찾는 연산, 집합의 루트 노드경로를 짧게 압축 시킴
- Union : x와 y가 포함되어 있는 집합을 합치는 연산
동작 방법
1. union 연산 확인 : 서로 연결된 두 노드를 확인
1-1. A의 루트 노드 A'와 B루트노드 B'를 찾는다(find)
2-2. A'를 B'의 부모 노드로 설정
2. 모든 연산을 처리할때까지 1번 반복
ex) {1,2,3,4,5,6}의 집합과 4개의 union 연산
union 1,4
union 2,3
union 1,2
union 5,6
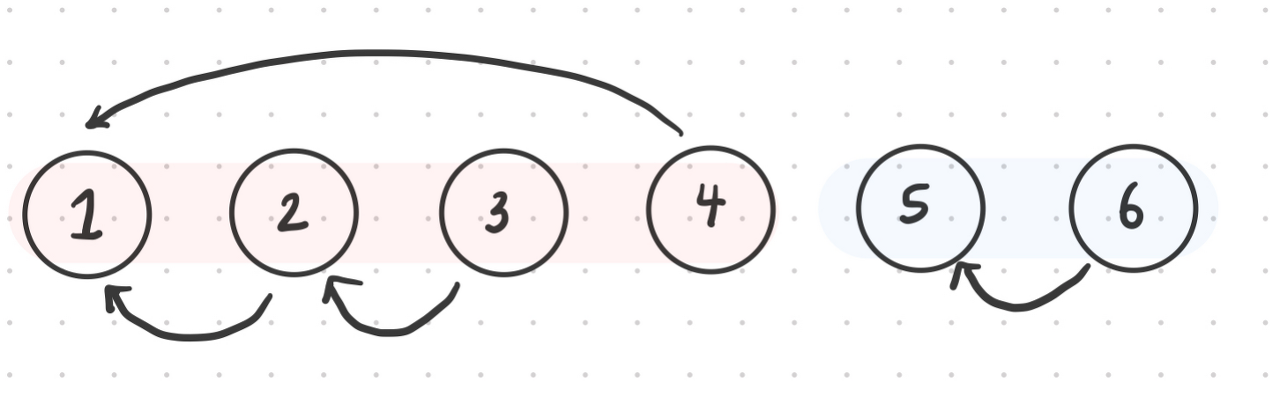

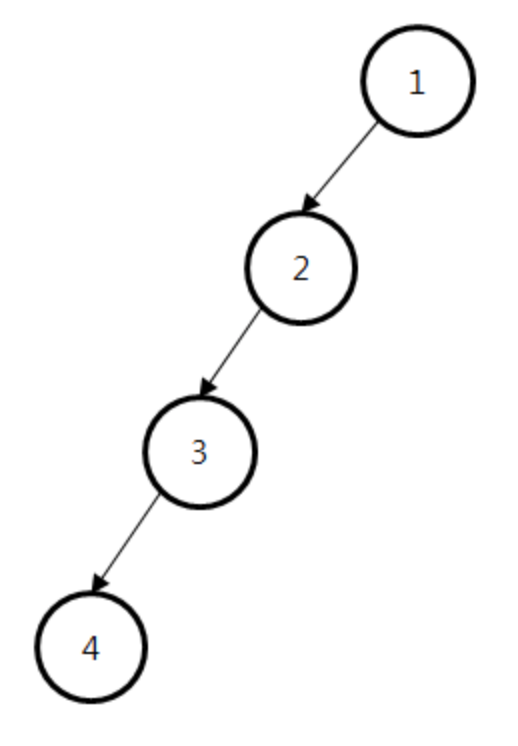
문제점
편향된 트리, 연결리스트로 연결된 형태로 나타나게 되면 탐색시 O(n)의 시간복잡도를 가지게 됨
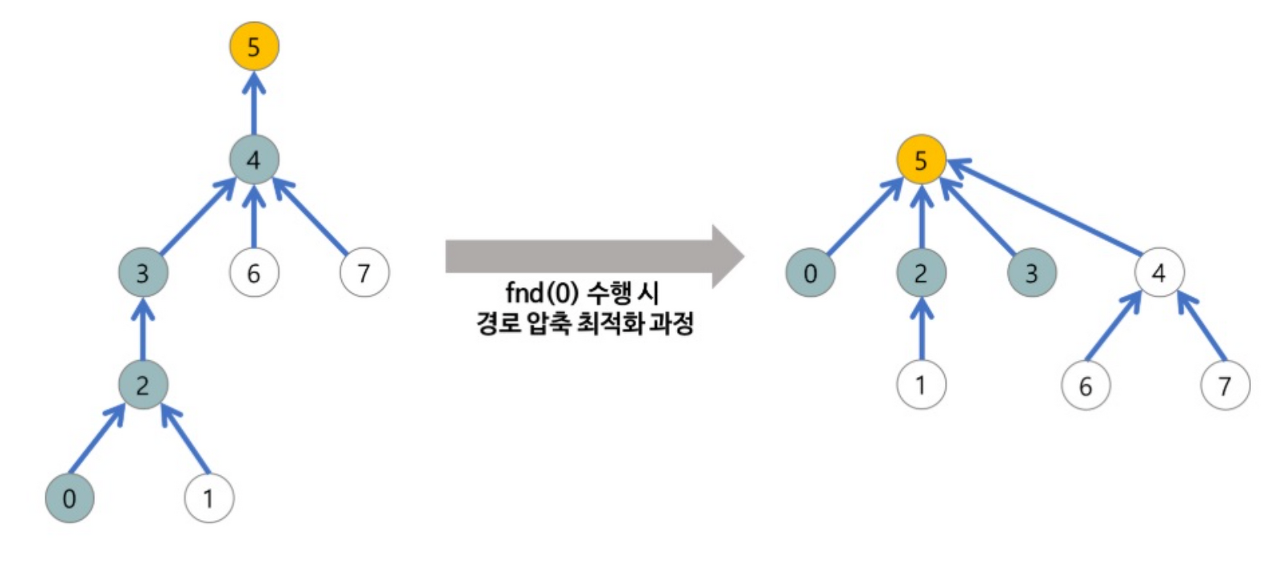
경로 압축 최적화
- 루트 노드인 Y를 찾았으면 X의 부모를 바로 루트 노드로 바꿈
- 파인드 함수를 거쳐간 노드들을 루트를 가르키게 함
- 결과적으로 트리의 높이가 압축되어 find함수의 효율을 높일 수 있음
시간복잡도
평균적으로 트리의 높이만큼 탐색하는 O(logN)
편향트리의 경우 시간 복잡도는 O(N)
경로 압축을 한 find의 시간 복잡도는 O(a(N)) (a(N)은 아커만 함수를 의미)
아커만 함수에서 N이 2^65536일 때, 아커만 함수의 값은 5가 되므로 상수의 시간 복잡도를 가짐
'자료구조' 카테고리의 다른 글
| 허프만 코드 (Huffman code) (0) | 2021.05.15 |
|---|---|
| 동적계획법 (Dynamic Programming) (0) | 2021.05.15 |
| 레드 블랙 트리 (RED-Black Tree) (0) | 2021.05.15 |
| 브루트 포스 알고리즘 (brute force), 백트래킹 (Backtracing) 알고리즘 (0) | 2021.05.12 |
| 벨만 포드 (Bellman-Ford) 알고리즘 (0) | 2021.05.12 |